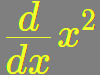5.4.1 Arithmetic Properties 🔧
Constant Rule
$$\frac{d}{dx}(C)=0$$
Constant Multiple Rule
$$\frac{d}{dx}(C\cdot f(x))=C\cdot \frac{d}{dx}f(x)$$
Sum & Difference Rules
$$\frac{d}{dx}\big(f(x)\pm g(x)\big)=f'(x)\pm g'(x)$$
5.4.2 Product Rule 🔧
$$\frac{d}{dx}\big(f(x)\cdot g(x)\big)=f'(x)\cdot g(x)+f(x)\cdot g'(x)$$
Proof
Insert the product expression into the derivative function
$$\lim\limits_{\Delta x\to 0}\frac{f(x+\Delta x)\cdot g(x+\Delta x)-f(x)\cdot g(x)}{\Delta x}$$
Add $f(x+\Delta x)\cdot g(x)$ minus itself into the numerator
$$\lim\limits_{\Delta x\to 0}\frac{f(x+\Delta x)\cdot g(x+\Delta x)+f(x+\Delta x)\cdot g(x)-f(x+\Delta x)\cdot g(x)-f(x)\cdot g(x)}{\Delta x}$$
Separate the fraction and apply the limit of sums property
$$\lim\limits_{\Delta x\to 0}\bigg(\frac{f(x+\Delta x)\cdot g(x+\Delta x)-f(x+\Delta x)\cdot g(x)}{\Delta x}\bigg)+\lim\limits_{\Delta x\to 0}\bigg(\frac{f(x+\Delta x)\cdot g(x)-f(x)\cdot g(x)}{\Delta x}\bigg)$$
Factor each term to isolate derivative functions
$$\lim\limits_{\Delta x\to 0}\bigg(f(x+\Delta x)\cdot\frac{g(x+\Delta x)-g(x)}{\Delta x}\bigg)+\lim\limits_{\Delta x\to 0}\bigg(g(x)\cdot\frac{f(x+\Delta x)-f(x)}{\Delta x}\bigg)$$
Rewrite in terms of derivatives
$$\bigg(\lim\limits_{\Delta x\to 0}f(x+\Delta x)\bigg)\cdot\bigg(\frac{d}{dx}g(x)\bigg)+\bigg(\lim\limits_{\Delta x\to 0}g(x)\bigg)\cdot\bigg(\frac{d}{dx}g(x)\bigg)$$
Solve the limits
5.4.3 Quotient Rule 🔧
$$\frac{d}{dx}\bigg(\frac{f(x)}{g(x)}\bigg)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)^2}$$
Proof
Insert the quotient expression into the derivative function
$$\lim\limits_{\Delta x\to 0}\frac{1}{\Delta x}\cdot\bigg(\frac{f(x+\Delta x)}{g(x+\Delta x)}-\frac{f(x)}{g(x)}\bigg)$$
Factor
$$\lim\limits_{\Delta x\to 0}\frac{f(x+\Delta x)\cdot g(x)-f(x)\cdot g(x+\Delta x)}{g(x)\cdot g(x+\Delta x)}$$
Add $f(x)\cdot g(x)$ minus itself into the numerator
$$\lim\limits_{\Delta x\to 0}\frac{f(x+\Delta x)\cdot g(x)+f(x)\cdot g(x)-f(x)\cdot g(x)-f(x)\cdot g(x+\Delta x)}{g(x)\cdot g(x+\Delta x)}$$
Separate the fraction and apply the limit of sums property
$$\lim\limits_{\Delta x\to 0}\frac{f(x+\Delta x)\cdot g(x)-f(x)\cdot g(x)}{g(x)\cdot g(x+\Delta x) \cdot\Delta x}+\lim\limits_{\Delta x\to 0}\frac{f(x)\cdot g(x)-f(x)\cdot g(x+\Delta x)}{g(x)\cdot g(x+\Delta x)\cdot\Delta x}$$
Cancel $g(x)$ in the first term
$$\lim\limits_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{g(x+\Delta x) \cdot\Delta x}+\lim\limits_{\Delta x\to 0}\frac{f(x)\cdot g(x)-f(x)\cdot g(x+\Delta x)}{g(x)\cdot g(x+\Delta x)\cdot\Delta x}$$
Factor a negative from the second term
$$\lim\limits_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{g(x+\Delta x) \cdot\Delta x}-\lim\limits_{\Delta x\to 0}\frac{f(x)\cdot g(x+\Delta x)-f(x)\cdot g(x)}{g(x)\cdot g(x+\Delta x)\cdot\Delta x}$$
Factor each term to isolate derivative functions
$$\lim\limits_{\Delta x\to 0}\bigg(\frac{1}{g(x+\Delta x)}\cdot\frac{f(x+\Delta x)-f(x)}{\Delta x}\bigg)-\lim\limits_{\Delta x\to 0}\bigg(\frac{f(x)}{g(x)\cdot g(x+\Delta x)}\cdot\frac{g(x+\Delta x)-g(x)}{\Delta x}\bigg)$$
Rewrite in terms of derivatives
$$\lim\limits_{\Delta x\to 0}\bigg(\frac{1}{g(x+\Delta x)}\bigg)\cdot\bigg(\frac{d}{dx}f(x)\bigg)-\lim\limits_{\Delta x\to 0}\bigg(\frac{f(x)}{g(x)\cdot g(x+\Delta x)}\bigg)\cdot\bigg(\frac{d}{dx}g(x)\bigg)$$
Solve the limits
$$\frac{1}{g(x)}\cdot\frac{d}{dx}f(x)-\frac{f(x)}{g(x)^2}\cdot\frac{d}{dx}g(x)$$
Factor
5.4.4 Power Rule 🔧
$$\frac{d}{dx}x^n=n\cdot x^{n-1},\medspace \forall x\isin\R$$
Proof
Insert the exponential expression into the derivative function
$$\frac{d}{dx}x^n=\lim\limits_{\Delta x\to 0}\frac{(x+\Delta x)^n-x^n}{\Delta x}$$
Apply binomial expansion to the numerator
$$\frac{d}{dx}x^n=\lim\limits_{\Delta x\to 0}\frac{1}{\Delta x}\cdot\binom{n}{1}\cdot x^{n-1}\cdot\Delta x+\binom{n}{2}\cdot x^{n-2}\cdot\Delta x^2+...+\Delta x^n$$
Simplify
$$\frac{d}{dx}x^n=\lim\limits_{\Delta x\to 0}\binom{n}{1}\cdot x^{n-1}+\binom{n}{2}\cdot x^{n-2}\cdot\Delta x+...+\Delta x^{n-1}$$
Solve the limit
$$\frac{d}{dx}x^n=\binom{n}{1}\cdot x^{n-1}$$
Calculate the binomial
5.4.5 Mean Value Theorem for Derivatives 🔧
Within $[a,b]$, there exists a point $c$ such that $f'(c)$ is equal to the function's average rate of change
$$f'(c)=\frac{f(b)-f(a)}{b-a}$$

5.4.6 Implicit Differentiation (Chain Rule) 🔧
$$\frac{d}{dx}f\big(g(x)\big)=f'\big(g(x)\big)\cdot g'(x)$$
$$\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}$$
Proof
5.4.7 Derivative of an Inverse Function 🔧
$$\big(f^{-1}\big)'\big(f(x)\big)=\frac{1}{f'(x)},\medspace f'(x)\ne 0$$
Proof
Using Langrange notation for $y=f(x)$, insert the inverse expression into the derivative function
$$(f^{-1})'(y)=\lim\limits_{\Delta y\to 0}\frac{f^{-1}(y+\Delta y)-f^{-1}(y)}{\Delta y}$$
Factor $y-y$ into the denominator
$$(f^{-1})'(y)=\lim\limits_{\Delta y\to 0}\frac{f^{-1}(y+\Delta y)-f^{-1}(y)}{y+\Delta y-y}$$
$y=f(x)\therefore f^{-1}(y)=x$. Substitute the inverse functions and $y$ values in terms of $x$.
$$(f^{-1})'(y)=\lim\limits_{\Delta y\to 0}\frac{x+\Delta x-x}{f(x+\Delta x)-f(x)}$$
Cancel like terms
$$(f^{-1})'(y)=\lim\limits_{\Delta y\to 0}\frac{\Delta x}{f(x+\Delta x)-f(x)}$$
Apply the reciprocal rule of division
$$(f^{-1})'(y)=1\bigg/\lim\limits_{\Delta y\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$
Rewrite the derivative function in terms of its differential
5.4.8 L'Hôpital's Rule 🔧
$$\text{If }\lim\limits_{x\to a}f(x)=\text{If }\lim\limits_{x\to a}g(x)=(0\text{ or }\pm\infin)$$
$$\text{then }\lim\limits_{x\to a}\frac{f(x)}{g(x)}=\lim\limits_{x\to a}\frac{f'(x)}{g'(x)}$$
The indeterminate form $0\cdot\infin$
The rule holds when applying the reciprocal rule of division; $x\cdot y\to y/(1/x)$, also taking into account that 0 becomes ∞ or ∞ becomes 0
The indeterminate form $\infin-\infin$
The rule holds when factoring terms into one fraction, given that ∞ is the result of division by 0
Exponential Indeterminate Forms
In the cases of $\lim_{x\to a}f(x)^{g(x)}=(1^\infin\medspace\lor\medspace 0^0\medspace\lor\medspace\infin^0)$, the natural logarithm can be taken and equated with another limit $L$, then antilogged
$$\lim\limits_{x\to a}g(x)\cdot\ln\big(f(x)\big)=\lim\limits_{x\to a}\frac{\ln\big(f(x)\big)}{1/g(x)}=\lim\limits_{x\to a}\frac{g(x)}{1/\ln\big(f(x)\big)}=L$$
$$\lim\limits_{x\to a}f(x)^{g(x)}=e^L$$
Proof
Lef $f'(x)$ and $g'(x)$ be continuous at $a$, and $f(a)=g(a)=0$ so that
$$\lim\limits_{x\to a}\frac{f'(x)}{g'(x)}=\frac{f'(x)}{g'(x)}$$
Apply the mean value theorem for derivatives
$$\lim\limits_{x\to a}\frac{f'(x)}{g'(x)}=\lim\limits_{x\to a}\bigg(\frac{f(x)-f(a)}{x-a}\bigg)\bigg/\bigg(\frac{g(x)-g(a)}{x-a}\bigg)$$
Simplify
$$\lim\limits_{x\to a}\frac{f'(x)}{g'(x)}=\lim\limits_{x\to a}\frac{f(x)-f(a)}{g(x)-g(a)}$$
Evaluate the limit
$$\lim\limits_{x\to a}\frac{f'(x)}{g'(x)}=\frac{0}{0}=\frac{f(x)}{g(x)}$$
Beginning using the reciprocal rule of division yields
$$\lim\limits_{x\to a}\frac{1/f'(x)}{1/g'(x)}=\frac{\infin}{\infin}=\frac{1/f(x)}{1/g(x)}$$
5.4.9 $d/dx\thinspace e^x$ 🔧
$$\frac{d}{dx}e^x=e^x$$
Proof
Insert $e^x$ into the derivative function
$$\lim\limits_{\Delta x\to 0}\frac{e^{x+\Delta x}-e^x}{\Delta x}$$
Factor the exponential power
$$\lim\limits_{\Delta x\to 0}\frac{e^x\cdot e^{\Delta x}-e^x}{\Delta x}$$
Factor e^x from the limit
$$e^x\cdot\lim\limits_{\Delta x\to 0}\frac{e^{\Delta x}-1}{\Delta x}$$
Evaluate using the
$e\thickspace$limit
5.4.A Derivative of Logarithmic Functions 🔧
$$\frac{d}{dx}=\log_b x=\big(x\cdot\ln(b)\big)^{-1}$$
$$\frac{d}{dx}\ln(x)=x^{-1}$$
$$x>0\medspace\land\medspace b\ne1$$
Proof
5.4.B Derivative of Exponential Functions 🔧
$$\frac{d}{dx}b^x=b^x\cdot\ln(b)$$
Proof
Let $y=b^x$ so that $\ln(y)=\ln(b^x)$, then use the logarithms power rule
$$\ln(y)=x\cdot\ln(b)$$
Derive
$$\frac{d}{dx}\ln(y)=\frac{d}{dx}x\cdot\ln(b)$$
Apply the chain rule to the left
$$y^{-1}\cdot\frac{dy}{dx}=\frac{d}{dx}x\cdot\ln(b)$$
Evaluate the derivative on the right
$$y^{-1}\cdot\frac{dy}{dx}=\ln(b)$$
Multiply by $y$
$$\frac{dy}{dx}=y\cdot\ln(b)$$
Substitute $b^x$ for $y$
5.4.C $d/dx\thinspace x^x$ 🔧
$$\frac{d}{dx}x^x=x^x\cdot \big(1+\ln(x)\big)$$
Proof