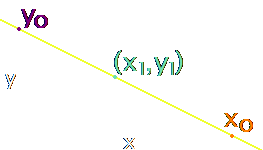3.1 Contents

1. Universal Properties

2. Systems of Linear Equations

3. Matrix Notation

3.1.1 Universal Properties

Slope of a line	$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$
Midpoint formula	$\big(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\big)$
Horizontal line	$y=c, \medspace m=0$
Vertical line	$x=c, \medspace m=±∞$
General equation	$A·x+B·y=C, \medspace x_∘=\frac{C}{A} \land y_∘=\frac{C}{B}$
Slope-intercept equation	$y(x)=m·x+y_∘$
Point-slope equation	$y-y_1=m·(x-x_1)$
Two point equation	$y-y_1=\frac{y_2-y_1}{x_2-x_1}·(x-x_1)$
Two-intercept equation	$\frac{x}{x_∘}+\frac{y}{y_∘}=1, \medspace x_∘≠0 \land y_∘≠0$

Proof of Two-Intercept Equation

Use the coordinates for the intercepts in the slope of a line equation, which are interchangeable $$m=\frac{0-y_∘}{x_∘-0}=\frac{y_∘-0}{0-x_∘}=-\frac{y_∘}{x_∘}$$ Substitute it into the slope-intercept equation $$y=y_∘-\frac{y_∘}{x_∘}·x$$ Divide by $y_∘$ and isolate $1$

3.1.2 Systems of Linear Equations

Two Line Relations

Two equations that intersect will have the same $(x,y)$ coordinates and different slopes

Parallel lines	$m_1=m_2$
Intercepting lines	$m_1 \ne m_2$
Perpendicular lines	$m_1=-1/m_2$

Intersection Solves by Addition

Two equations may be added to each other. Like variables must be on the same side of the equation. $$\begin{array}{r} -2·x+9·y=5\\ \phantom{-}2·x-5·y=3\\ \overline{\phantom{-3·x+}4·y=8}\\ \end{array}$$ When one variable is solved, its value can be plugged into either of the equations to solve for the other variable. If the solution appears as $0=n$, then the lines are parallel.

Intersection Solves by Isolation

Given two equations with different slopes $$y=m_1·x+y_1\qquad y=m_2·x+y_2$$ To solve for $x$, set the equations equal to each other $$m_1·x+y_1=m_2·x+y_2$$ Subtract $y_1$ and $m_2·x$ $$m_1·x-m_2·x=y_2-y_1$$ Factor $$(m_1-m_2)·x=y_2-y_1$$ Isolate $x$ $$x=\frac{y_2-y_1}{m_1-m_2}$$ The value of $x$ can be plugged into either of the equations to solve for $y$. If the solution appears as $n/0$, then the lines are parallel.

3.1.3 Matrix Notation

A matrix can be used to display the coefficients of linear expressions $$ \begin{array}{c} 3·x+2·y \\ 4·x-1·y \end{array} ↔ \begin{bmatrix} 3 & \phantom{0}2 \\ 4 & -1 \end{bmatrix} $$ A joined matrix can be used to display the coefficients of linear eqautions in the general form, with the constants in a separate column $$ \begin{array}{c} 3·x+2·y=25 \\ 4·x-1·y=\phantom{0}4 \end{array} ↔ \begin{bmatrix} \begin{array}{cc|c} 3 & \phantom{-}2 & 25 \\ 4 & -1 & \phantom{0}4 \end{array} \end{bmatrix} $$

Row Operations

A joined matrix representing linear equations allows for certain arithmetical operations on individual rows

1. Multiplication of a row $$ \begin{array}{cc} \\ 2 & · \end{array} \begin{bmatrix} \begin{array}{cc|c} 3 & \phantom{-}2 & 25 \\ 4 & -1 & \phantom{0}4 \end{array} \end{bmatrix} = \begin{bmatrix} \begin{array}{cc|c} 3 & \phantom{-}2 & 25 \\ 8 & -2 & \phantom{0}8 \end{array} \end{bmatrix} $$ 2. Addition of one row to another $$ \begin{array}{c} \text{R1} \\ \text{R2} \end{array} \begin{bmatrix} \begin{array}{cc|c} 3 & \phantom{-}2 & 25 \\ 8 & -2 & \phantom{0}8 \end{array} \end{bmatrix} $$ $$ \begin{array}{c} \text{R1\phantom{+R2}} \\ \text{R1+R2} \end{array} \begin{bmatrix} \begin{array}{cc|c} \phantom{0}3 & 2 & 25 \\ 11 & 0 & 33 \end{array} \end{bmatrix} $$ 3. Switching rows $$ \begin{bmatrix} \begin{array}{cc|c} 11 & 0 & 33 \\ \phantom{0}3 & 2 & 25 \end{array} \end{bmatrix} $$ The aim is to create a matrix to display the values for $(1·x,1·y)$ in the column with constants. If this is unattainable, then the lines are parallel.

Example

To continue solving for the above, divide row 1 by 11 $$ \begin{bmatrix} \begin{array}{cc|c} 1 & 0 & \phantom{0}3 \\ 3 & 2 & 25 \end{array} \end{bmatrix} $$ Add row 1 multiplied by –3 to row 2 $$ \begin{bmatrix} \begin{array}{cc|c} 1 & 0 & \phantom{0}3 \\ 0 & 2 & 16 \end{array} \end{bmatrix} $$ Divide row 2 by 2 $$ \begin{bmatrix} \begin{array}{cc|c} 1 & 0 & 3 \\ 0 & 1 & 8 \end{array} \end{bmatrix} $$ The two equations intersect at $(x,y)=(3,8)$