1.3 Contents

1. Terminology

2. The Term "General"

3. Definitions

4. Transformations

1.3.1 Terminology

$17+5=22$	sum
$17-5=12$	difference
$17·5=22$	product
$\frac{17}{5}=3+\frac{2}{5}$	$17$: dividend $5$: divisor $17/5$: simplified fraction $3$: quotient $2$: remainder $3+2/5$: proper fraction
$\frac{x}{x_∘}+\frac{y}{y_∘}=1$	$x$: abscissa $x_∘$: horizontal axis intercept $+$: operator $y$: ordinate $y_∘$: vertical axis intercept $1$: value
$y=a·x^2+b·x+c$	$y$: dependent variable $a$: leading coefficient $x$: independent variable $2$: order $b$: coefficient $c$: constant
$(a+b·i)(a-b·i)=a^2+b^2$	( expression = expression ) ← equation factored form = expanded form $a$: real component $b·i$: imaginary component $(a±b·i)$: roots $(a+b·i)(conjugate)$
$\sqrt[n]{x}$	$n$: $n$th root $x$: radicand
$x/x_∘$ $y/y_∘$ $a·x^2$ $b·x$ $(a±b·i)$ $a^2$ $b^2$ $\sqrt[n]{x}$	terms

1.3.2 The Term "General"

General means that all possible situations are represented or that something applies to multiple scenarios.

Example 1

Using the quadratic formula to solve for:

$$x=\frac{-b \pm \sqrt{b^2-4·a·y_∘}}{2·a}$$ $$x=\frac{-b \pm \sqrt{b^2+4·a·(y-y_∘)}}{2·a}$$

Example 2

The conic sections general formula describes ellipses, circles, parabolas, hyperbolas, and lines. $$A·x^2+B·x·y+C·y^2+D·x+E·y+F=0$$

1.3.3 Definitions

Even - symmetric about $y$-axis $$f(-x)=f(x)$$
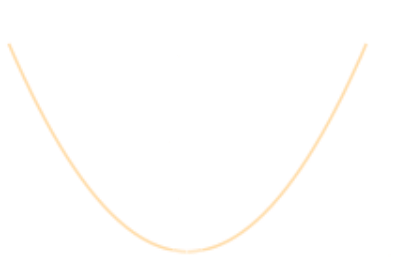Odd - symmetric about origin $$f(-x)=-f(x)$$
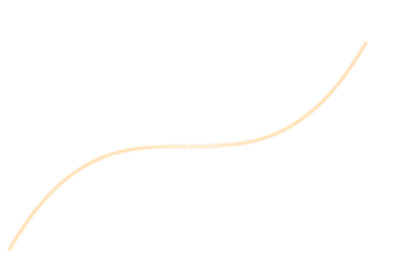Inverse - reflected about $y=x$ $$f^{-1}(f(x))=x$$
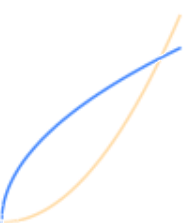Absolute value - magnitude; non-negative $$ |x| = \begin{cases} \phantom{-}x &x ≥ 0 \\ -x &x \lt 0 \end{cases} $$
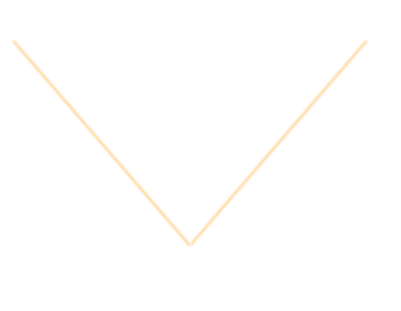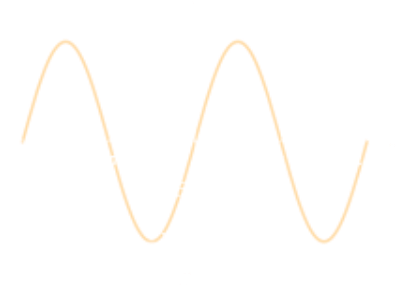
Periodic - repeated segment ($P$) $$f(x+P)=f(x)$$

1.3.4 Transformations

$$a\cdot f(b\cdot x+c)+d$$

• If $|a| \gt 1$, $f$ stretches vertically.
• If $|a| \lt 1$, $f$ compresses vertically.
• If $a \lt 0$, $f$ flips vertically.
• If $|b| \gt 1$, $f$ compresses horizontally.
• If $|b| \lt 1$, $f$ stretches horizontally.
• If $b \lt 0$, $f$ flips vertically.
• If $c \gt 0$, $f$ shifts to the left.
• If $c \lt 0$, $f$ shifts to the right.
• If $d \gt 0$, $f$ shifts upwards.
• If $d \lt 0$, $f$ shifts downwards.