5.1.1 Definition & Notation
Determinations of specific values in a function, even where values
don't exist.
$$\frac{x^2-4}{x-2}\medspace→\medspace\frac{2^2-4}{2-2}=\frac{0}{0}$$
| $$\lim\limits_{x\to a^+}f(x)$$ |
The limit as a function approaches a point from the right |
| $$\lim\limits_{x\to a^-}f(x)$$ |
The limit as a function approaches a point from the left |
| $$\lim\limits_{x\to a}f(x)$$ |
The limit as a function approaches a point from the both sides |
5.1.3 Arithmetic Properties
The limit of a constant function is equal to the constant
$$\lim\limits_{x\to a} c=c$$
The limit of a constant multiple of a function equals the product of the constant with the limit of the function
$$\lim\limits_{x\to a} c\cdot f(x)=c\cdot\lim\limits_{x\to a} f(x)$$
The limit of sums is the sum of the limits
$$\lim\limits_{x\to a} \big(f(x)\pm g(x)\big)=\lim\limits_{x\to a} f(x)\pm \lim\limits_{x\to a} g(x)$$
The limit of products is the product of the limits
$$\lim\limits_{x\to a} \big(f(x)\cdot g(x)^{\pm 1}\big)=\lim\limits_{x\to a} f(x)\cdot \lim\limits_{x\to a} g(x)^{\pm 1}$$
5.1.6 Limits of Trig Functions
$$\lim\limits_{\theta\to 0}\frac{\sin(\theta)}{\theta}=1\qquad\lim\limits_{\theta\to 0}\frac{\cos(\theta)-1}{\theta}=0$$
Proof of Sine Limit
Use the incircle of a
regular octagon with an apothem of magnitude 1 to define points in the sector for $0 \le \theta \le \pi/4$
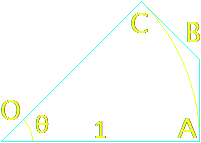
Add to the top right corner a triangular region, forming an overall right triangle
The following determination can be made inside of triangle $OAD$
$$\text{arc} AC \lt |AB|+|BC| \lt \big(|AB|+|BD|=|AD|\big)$$
$$\land \medspace |AD|=|OA|\cdot\tan(\theta)=\tan(\theta)$$
$$\therefore \text{arc} AC \lt\tan(\theta)$$
The apothem is $1$ and the arc length $AC$ is the angle $\theta$. Substitute tangent for its cofunctions, then isolate $\cos(\theta)$
$$\theta \lt \frac{\sin(\theta)}{\cos(\theta)} \medspace \to \medspace \cos(\theta) \lt \frac{\sin(\theta)}{\theta}$$
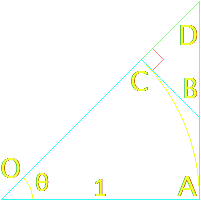
Connect point $C$ perpendicularly to $|OA|$ at point $E$, and connect a line segment to $|AC|$
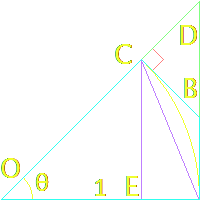
Note that $|CE|=|OC|\cdot\sin(\theta)=\sin(\theta)$ and $|CE|\lt |AC|\lt arc AC$. It follows that
$$\sin(\theta)\lt\theta\medspace\therefore\medspace\frac{\sin(\theta)}{\theta}\lt 1$$
Combine the two inequalities involving $\sin(\theta)/\theta$
$$\cos(\theta)\lt\frac{\sin(\theta)}{\theta}\lt 1$$
Apply the squeeze theorem for the limit on the right
$$\lim_{\theta\to 0^+}\cos(\theta)=1\medspace\land\medspace\lim_{\theta\to 0^+}1=1\medspace\therefore\medspace\lim_{\theta\to 0^+}\frac{\sin(\theta)}{\theta}=1$$
Sine is an odd function, so its nature tending to zero may be determined with sign reversal
$$\frac{\sin(-\theta)}{-\theta}=\frac{-\sin(\theta)}{-\theta}=\frac{\sin(\theta)}{\theta}$$
Since the function is the same from the reverse direction, the limit exists
$$\lim_{\theta\to 0^-}\frac{\sin(\theta)}{\theta}=\lim_{\theta\to 0^+}\frac{\sin(\theta)}{\theta}=\lim_{\theta\to 0}\frac{\sin(\theta)}{\theta}=1$$
Proof of Cosine Limit
Given the cosine limit, multiply by its conjugate
$$\lim\limits_{x\to 0}\frac{\cos(\theta)-1}{\theta}\cdot \frac{\cos(\theta)+1}{\cos(\theta)+1}$$
Factor
$$\lim\limits_{x\to 0}\frac{\cos^2(\theta)-1}{\theta\cdot(\cos(\theta)+1)}$$
Apply the
right angle identity for sine
$$\lim\limits_{x\to 0}\frac{-\sin^2(\theta)}{\theta\cdot(\cos(\theta)+1)}$$
Isolate $\sin(\theta)/\theta$ with the
limit of products
$$\lim\limits_{x\to 0}\frac{-\sin(\theta)}{\cos(\theta)+1}\cdot\lim\limits_{\theta\to 0}\frac{\sin(\theta)}{\theta}$$
Evaluate the limits
$$\frac{0}{2}\cdot 1$$
