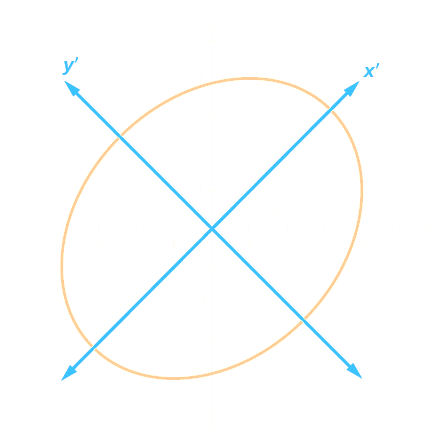3.5.1 Universal Properties
Two-dimensional subsets of a 3D (double) cone surface in which the shapes are determined by the intersection of a 2D plane

General Equation
$$A⋅x^2+B⋅x⋅y+C⋅y^2+D⋅x+E⋅y+F=0$$
All conic sections will be represented without rotation until the section on rotations. In other words, $B=0$.
Discriminant & Related Properties
$$\Delta=B^2-4⋅A⋅C$$
Assuming no other values:
-
If $B=0$, the function is even either vertically or horizontally (not rotated)
-
If $Δ \lt 0$, the function is an ellipse
-
If $Δ \lt 0$, $B=0$, and $A \lt C$, the function is an ellipse with a horizontal major axis
-
If $Δ \lt 0$, $B=0$, and $A \gt C$, the function is an ellipse with a vertical major axis
-
If $Δ \lt 0$, $B=0$, and $A=C$, the function is a circle
-
If $Δ \lt 0$, $A=C$, $B=D=E=0$, the function is a circle centered at the origin
-
If $Δ=0$, the function is a parabola
-
If $C=D=F=0$, the function is a vertical parabola with the vertex at the origin
-
If $A=E=F=0$, the function is a horizontal parabola with the vertex at the origin
-
If $D=E=0$, the function is either an ellipse or hyperbola centered at the origin
-
If $Δ \gt 0$, the function is a hyperbola
-
If $Δ \gt 0$ and $A+C=0$, the function is a rectangular hyperbola, meaning the asymptotes are perpendicular
Focus, Directrix & Eccentricity
A focus/foci is a point or set of points around which a curve is guided
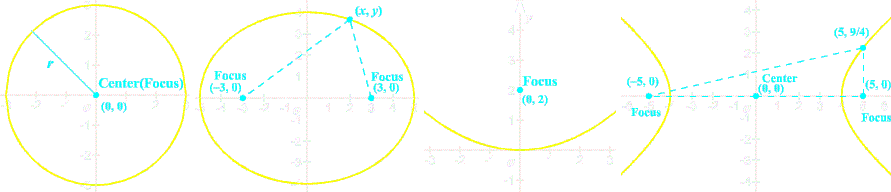
A Directrix is a fixed line perpendicular to the (major) axis of a function, which is determined by its focus and curvature
Eccentricity is a function's deviation from being circular, and a constant ratio given by $e=c/a$;
$$\text{eccentricity}=\frac{\text{distance from any point to the focus}}{\text{distance from any point to the directrix}}$$
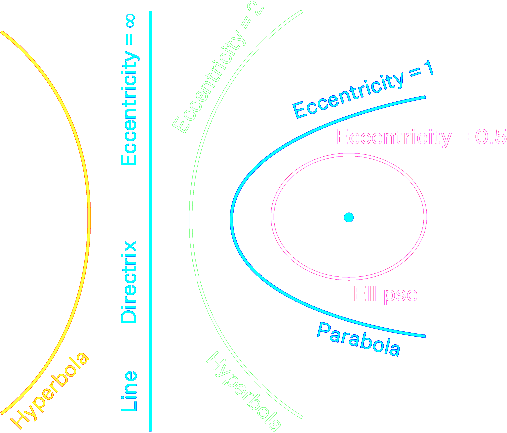
Image taken from
CueMath and edited
-
Two conic sections are congruent if the eccentricity of each are equal
-
Circle eccentricities are always 0
-
Ellipse eccentricities are always between 0 and 1
-
Parabola eccentricities are always 1
-
Hyperbola eccentricities are always between 1 and ∞
-
Line eccentricities are always ∞
Degenerate Conics
Conics when either a 2D plane intercepts the vertex of a double cone, or the result of the general equation yields a non-function by real algebraic definition
| No result |
$A⋅x^2+A⋅y^2+1=0$ |
| Point |
$A⋅x^2+A⋅y^2=0$ |
| Line |
$D⋅x+E⋅y+F=0$ |
| Intersecting lines |
$x^2-y^2=0$ |
| Parallel lines |
$x^2-1=0$ |
3.5.2 Circles
Closed curves with all points equidistant to an internal point
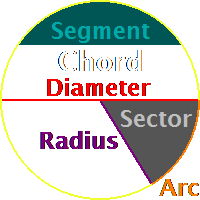
| Circumference |
$2\cdot\pi\cdot r$ |
| Area |
$\pi\cdot r^2$ |
| Arc length |
$\theta\cdot r$ |
| Sector area |
$\theta\cdot r^2/2$ |
| Chord length (k) |
$2\cdot r\cdot \sin\Big(\frac{\theta}{2}\Big)$ |
| Segment area |
$\frac{r^2}{2}\cdot\Big(\theta-2\cdot\sin\Big(\frac{\theta}{2}\Big)\cdot\cos\Big(\frac{\theta}{2}\Big)\Big)$ |
| Conic general equation |
$A\cdot(x^2+y^2)+D\cdot x+E\cdot y+F=0,A≠0$ |
| Standard equation |
${(x-x_\circ)}^2+{(y-y_\circ)}^2=r^2$ |
| Conic-standard conversions |
$x_\circ=-D/(2\cdot A)$
$y_\circ=-E/(2\cdot A)$
$r^2=(D^2+E^2-4\cdot A\cdot F)/(4\cdot A^2)$ |
| Focus Coordinates |
$(x_\circ,y_\circ)$ |
| Eccentricity |
$0$ |
| Directrix |
None |
Annulus
A ring formed by two concentric circles in which all features of circles apply with respect to differences involving two radii
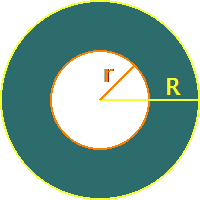
| Perimeter |
$2\cdot\pi\cdot(R+r)$ |
| Area |
$\pi\cdot(R^2-r^2)$ |
| Sector Area |
$\theta\cdot(R^2-r^2)/2$ |
Deductive Logic for Area
Apply the
area function of regular polygons, using the circumference as the perimeter and the radius as the apothem
$$A=(2\cdot\pi\cdot r)\cdot\frac{r}{2}$$
Proof of Arc Length
The arc length is a fraction of the circumference, therefore can be found by the ratio to it and its angle
$$\frac{a}{2\cdot\pi\cdot r}=\frac{\theta}{2\cdot\pi}$$
Proof of Sector Area
The sector area is a fraction of the circle area, therefore can be found by the ratio to it and its angle
$$\frac{A_S}{\pi\cdot r^2}=\frac{\theta}{2\cdot\pi}$$
Proof of Chord Length
Use the radius and half the chord length to form a right triangle
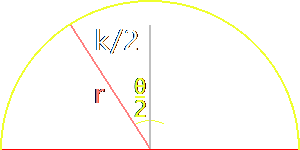
Use the
sine function for the angle
$$\sin\Big(\frac{\theta}{2}\Big)=\frac{k}{2\cdot r}$$
Multiply by $2\cdot r$
Proof of Segment Area
The segment area is the sector area minus the
triangular area between the center and chord
$$A_S=\frac{\theta\cdot r^2}{2}-A_t$$
For the triangular area, use the chord length equation for the base and
right angle definition with respect to the radius to find the height
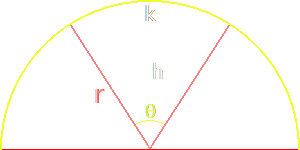
|
$$k=2\cdot r\cdot\sin\Big(\frac{\theta}{2}\Big)$$
$$h=r\cdot\cos\Big(\frac{\theta}{2}\Big)$$
|
Substitute the triangular area using these values for $(k\cdot h)/2$
$$A_S=\frac{\theta\cdot r^2}{2}-\frac{r^2}{2}\cdot 2\cdot\sin\Big(\frac{\theta}{2}\Big)\cdot\cos\Big(\frac{\theta}{2}\Big)$$
Factor
$$A_S=\frac{r^2}{2}\cdot\Big(\theta-2\cdot\sin\Big(\frac{\theta}{2}\Big)\cdot\cos\Big(\frac{\theta}{2}\Big)\Big)$$
Conic-Standard Conversion
Given the
conic general equation with the properties for a circle, group the $x$ terms and $y$ terms, and isolate the constant
$$A\cdot x^2+D\cdot x+A\cdot y^2+E\cdot y=-F$$
Divide by $A$
$$x^2+\frac{D}{A}\cdot x+y^2+\frac{E}{A}\cdot y=-\frac{F}{A}$$
Complete the square for the $x$ and $y$ terms
$$x^2+\frac{D}{A}\cdot x+\frac{D^2}{4\cdot A^2}+y^2+\frac{E}{A}\cdot y+\frac{E^2}{4\cdot A^2}=-\frac{F}{A}+\frac{D^2}{4\cdot A^2}+\frac{E^2}{4\cdot A^2}$$
Factor
$${\Big(x+\frac{D}{2\cdot A}\Big)}^2+{\Big(y+\frac{E}{2\cdot A}\Big)}^2=\frac{D^2+E^2-4\cdot A\cdot F}{4\cdot A^2}$$
Equate the coefficients to the standard equation
3.5.3 Ellipses
Closed ovular curves whose points are the result of a constant sum between two internal points
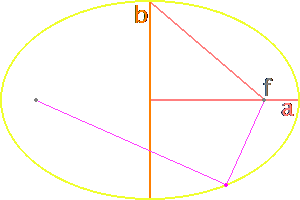
| Perimeter |
$4\cdot a\lt 2\cdot\pi\cdot a, a\gt b$ |
| Area |
$\pi\cdot a\cdot b$ |
| Conic General Equation |
$A\cdot x^2+C\cdot y^2+D\cdot x+E\cdot y+F=0,A\cdot C>0$ |
| Standard Equation |
${(x-x_\circ)}^2/a^2+{(y-y_\circ)}^2/b^2=1$ |
| Conic-Standard Conversions |
$A=b^2$
$C=a^2$
$D=-2\cdot b^2\cdot x_\circ$
$E=-2\cdot a^2\cdot y_\circ$
$F=b^2\cdot{x_\circ}^2+a^2\cdot{y_\circ}^2-a^2\cdot b^2$
$a^2=C$
$b^2=A$
$x_\circ=-D/(2\cdot A)$
$y_\circ=-E/(2\cdot C)$ |
| Orientation |
horizontal if $C>A \land a>b$
vertical if $A>C \land b>a$ |
| Center Coordinates |
$(x_\circ,y_\circ)$ |
| Foci Coordinates |
$f=\big(x_\circ\pm\sqrt{a^2-b^2}, y_\circ\big),a>b$
$f=\left(x_\circ,y_\circ\pm \sqrt{b^2-a^2}\right),b>a$ |
| Eccentricity |
$e=f/a=\sqrt{1-b^2/a^2},a>b$
$e=f/b=\sqrt{1-a^2/b^2},b>a$ |
| Directrix |
$x=\pm a/e,a>b$
$y=\pm b/e,b>a$ |
Conic-Standard Conversion
Given the standard equation
$$\frac{{(x-x_\circ)}^2}{a^2}+\frac{{(y-y_\circ)}^2}{b^2}=1$$
Multiply by $a^2\cdot b^2$
$$b^2\cdot{(x-x_\circ)}^2+a^2\cdot{(y-y_\circ)}^2=a^2\cdot b^2$$
Expand
$$b^2\cdot x^2-2\cdot b^2\cdot x\cdot x_\circ+b^2\cdot x_\circ^2+a^2\cdot y^2-2\cdot a^2\cdot y\cdot y_\circ+a^2\cdot y_\circ^2=a^2\cdot b^2$$
Rearrange to appear as the conic general equation
$$b^2\cdot x^2+a^2\cdot y^2-2\cdot b^2\cdot x_\circ\cdot x-2\cdot a^2\cdot y_\circ\cdot y+b^2\cdot x_\circ^2+a^2\cdot y_\circ^2-a^2\cdot b^2=0$$
Equate the coefficients to the conic equation
3.5.4 Parabolas
Open mirrored curves whose points are the same distance between a common internal point and an exterenal line.
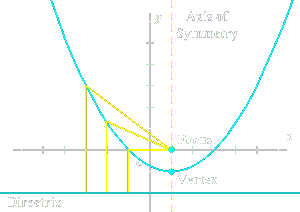
| Conic General Equations |
vertical: $A\cdot x^2+D\cdot x+E\cdot y+F=0$
horizontal: $C\cdot y^2+D\cdot x+E\cdot y+F=0$ |
|
The following are in vertical form
|
| Standard Equation |
$y=a\cdot x^2+b\cdot x+y_\circ$ |
| Vertex Equation |
$y=a\cdot(x-x_\circ)^2+y_\circ$ |
| Intercept Equation |
$y=a\cdot(x-x_1)(x-x_2)$ |
| Discriminant |
$\Delta=b^2-4\cdot a\cdot y_\circ$
If $Δ \lt 0$, two $x$-intercepts
If $Δ=0$, one $x$-intercept
If $Δ>0$, no $x$-intercepts |
| $x$ Relationships |
$x_1+x_2=-b/a$
$x_1-x_2=\sqrt{\Delta}/a$
$x_1\cdot x_2=y_\circ/a$ |
| Conic-Standard Conversion |
$a=-A/E$
$b=-D/E$
$y_\circ=-F/E$ |
| Vertex Coordinates |
$(x_\circ,y_\circ)=\big(-\frac{b}{2\cdot a},y_\circ-\frac{b^2}{4\cdot a}\big)$ |
| $x$-Intercepts |
$\lbrace (x_1,0),(x_2,0) \rbrace = \big(\frac{-b \pm \sqrt{b^2-4\cdot a\cdot y_\circ}}{2\cdot a},0\big)$ |
| Fucus Length from Vertex |
$f=\frac{1}{4\cdot a}$ |
| Focus Coordinates |
$\big(-\frac{b}{2\cdot a},y_\circ-\frac{b^2+1}{4\cdot a}\big)$ |
| Eccentricity |
$1$ |
| Drectrix |
$y=-f$ |
Conic-Standard Conversion
Rearrange the conic general equation to isolate the $y$ term
$$E\cdot y=-A\cdot x^2-D\cdot x-F$$
Divide by $E$
$$y=-\frac{A}{E}\cdot x^2-\frac{D}{E}\cdot x-\frac{F}{E}$$
Equate the coefficients to the standard equation
Standard-Vertex Conversion
Given the standard equation, isolate the $x$ terms
$$y-y_\circ=a\cdot x^2+b\cdot x$$
Divide by $a$
$$\frac{y-y_\circ}{a}=x^2+\frac{b\cdot x}{a}$$
Complete the square
$$\frac{y-y_\circ}{a}+\frac{b^2}{4\cdot a^2}=x^2+\frac{b\cdot x}{a}+\frac{b^2}{4\cdot a^2}$$
Factor
$$\frac{y-y_\circ}{a}+\frac{b^2}{4\cdot a^2}={\bigg(x+\frac{b}{2\cdot a}\bigg)}^2$$
Multiply by $a$
$$y-y_\circ+\frac{b^2}{4\cdot a}=a\cdot{\bigg(x+\frac{b}{2\cdot a}\bigg)}^2$$
Isolate $y$
$$y=a\cdot{\bigg(x+\frac{b}{2\cdot a}\bigg)}^2-\frac{b^2}{4\cdot a}+y_\circ$$
Equate the coefficients to the vertex equation
Standard-Intercept Conversion
Given the
quadratic formula with $y=0$, find the zeros of $x$
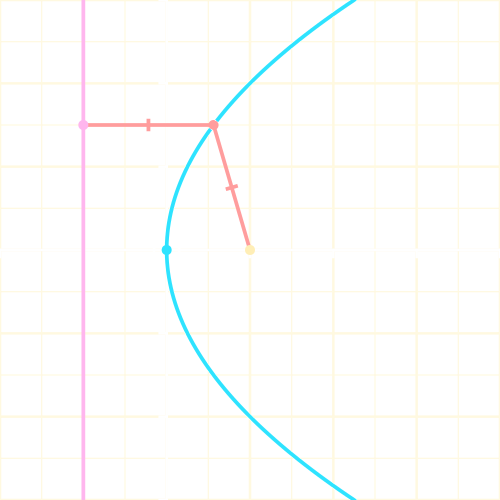
3.5.5 Hyperbolas
A mirrored set of open mirrored curvers whose points are the difference between two common internal points.
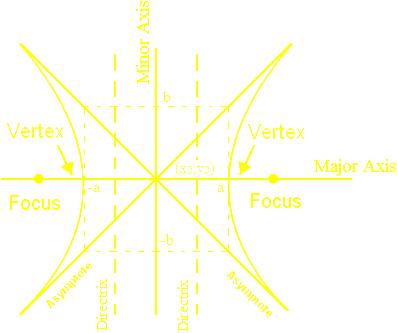
Image taken from
BYJU's and edited
| Conic General Equation |
$A\cdot x^2+C\cdot y^2+D\cdot x+E\cdot y+F=0, A\cdot C \lt 0$ |
| Standard Equation |
$(x-x_\circ)^2/a^2+(y-y_\circ)^2/b^2=1, a^2\cdot b^2 \lt 0$ |
| Standard Equation (Real Terms Only) |
$\pm (x-x_\circ)^2/a^2 \mp (y-y_\circ)^2/b^2=1$ |
| Conic-Standard Conversion |
$A=b^2$
$C=a^2$
$D=-2\cdot b^2\cdot x_\circ$
$E=-2\cdot a^2\cdot y_\circ$
$F=b^2\cdot{x_\circ}^2+a^2\cdot{y_\circ}^2-a^2\cdot b^2$
$a^2=C$
$b^2=A$
$x_\circ=-D/(2\cdot A)$
$y_\circ=-E/(2\cdot C)$ |
| Orientation |
horizontal if $C \lt 0; a \isin ℂ$
vertical if $A \lt 0; b \isin ℂ$ |
| Vertices |
$(x_\circ\pm a,y_\circ) \lor (x_\circ,y_\circ\pm b)$ |
| Focus Coordinates |
$(x_\circ\pm \sqrt{a^2+b^2},y_\circ) \lor (x_\circ,y_\circ \pm \sqrt{a^2+b^2})$ |
| Eccentricity |
$e=f/a=\sqrt{1+b^2/a^2}$ |
| Directrix |
$x=\pm a^2/f \lor y=\pm b^2/f$ |
| Asymptotes |
$y= \pm b\cdot(x-x_\circ)/a+y_\circ$ |
Conic-Standard Conversion
The proof is the same for
ellipses, however since by definition $A\cdot C \lt 0$, either $a$ or $b$ must be imaginary. For the real-numbers-only representation, one of the terms is negated for $a$ and $b$ to both be positive.
3.5.6 Rotations 🔧
Conic section rotations occur exclusively when in the
general equation $B \neq 0$
$$A\cdot x^2+B\cdot x\cdot y+C\cdot y^2+D\cdot x+E\cdot y+F=0$$
The angle of rotation is used to identify a new axis
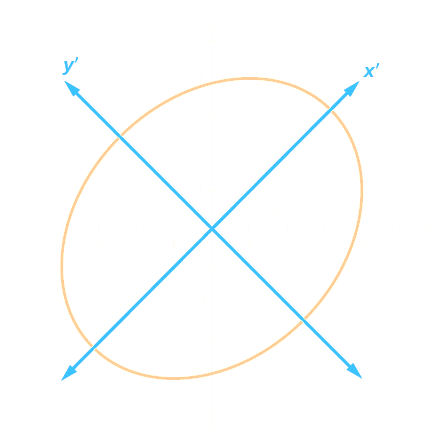
The original components are used to determine the new axis with respect to the angle of rotation
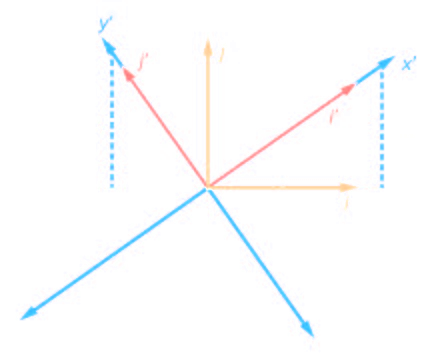
$$x=x'\cdot\cos(\theta)-y'\cdot\sin(\theta)$$
$$y=x'\cdot\sin(\theta)+y'\cdot\cos(\theta)$$
$$A\cdot\big( \big)^2+B\cdot\big( \big)\cdot\big( \big)+C\cdot\big( \big)^2+D\cdot\big( \big)+E\cdot\big( \big)+F=0$$
























 Use the sine function for the angle
$$\sin\Big(\frac{\theta}{2}\Big)=\frac{k}{2\cdot r}$$
Multiply by $2\cdot r$
Use the sine function for the angle
$$\sin\Big(\frac{\theta}{2}\Big)=\frac{k}{2\cdot r}$$
Multiply by $2\cdot r$